xlf EandA series

Price to return

Code development version. This document provides some assignment solution ideas, presented here as an exercise.

0. Preliminary

The EXERCISE - implement the following

1. Tasks

This is a code development version - that describes a series of tasks with suggested coding solutions. Note: "The "Close vector of the data test period" (from point B.2) is set to 10 observations in this version.

Task 1.1: P2R

Write a private function procedure with the following specifications:

• Name: P2R (an abbreviation of Price to Return)
• Arguments:
  1. Compulsory - accepts a VBA array, with suitable name and type
  2. Optional - named Ret (the default TRUE for log return, else FALSE for change in price)
• The function is only called from a VBA procedure, so the default value can be set in the function declaration line
• Argument 1 will always be an m x 1 column vector, with prices in ascending order. m is the number of elements
• The return value of returns is an array of dimension (m - 1) x 1

Option Explicit
Option Base 1

'' === B.1

Private Function P2R(Price() As Double, Optional Ret As Variant = True) As Variant
'' P2R: Price to return
'' Price: compulsory - a VBA array
'' Ret: optional - a Boolean. True (default) for log return
''                            False for delta price return

Dim LB As Integer, UB As Integer
Dim t As Integer
Dim RetArray() As Double

    '' Dimension the return value array
    LB = LBound(Price)
    UB = UBound(Price)
    ReDim RetArray(LB + 1 To UB, 1)

    If Ret = True Then
        '' Log returns
        For t = 1 To UB
            RetArray(t, 1) = Log(Price(t) / Price(t - 1))
        Next t
    Else
        '' Change in price
        For t = 1 To UB
            RetArray(t, 1) = (Price(t) - Price(t - 1)) / Price(t - 1)
        Next t
    End If

    P2R = RetArray

End Function

About Code 1

1. Line 6: function procedure declaration - Private function with 1. Compulsory argument, a VBA array (dynamic) named Price. 2. Optional argument named Ret as Variant with assigned default value equals True.
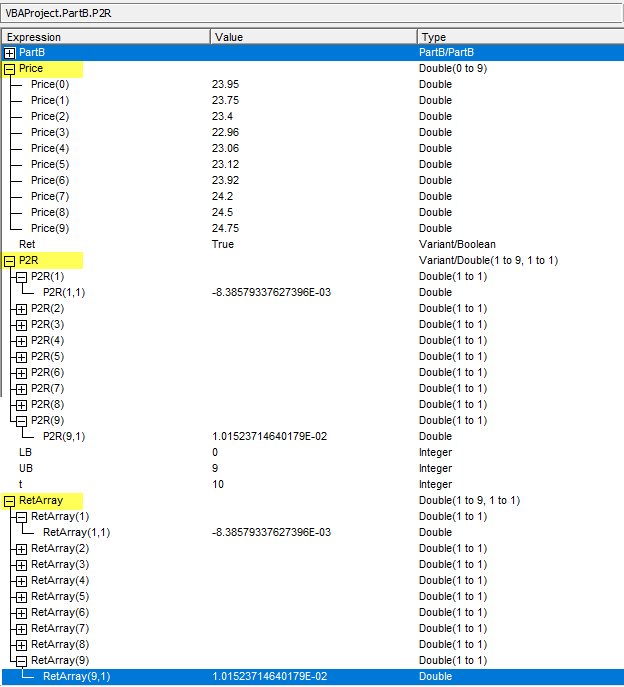
   • Price array is dynamic but does not need an associated Redim statement, because Price inherits the dimension of the Caller procedure. Code 2 passes a 9 element array (P Double(0 to 9)), thus Price() array has Type(dimension) Double(0 to 9) - see figure 1 for details
   • Ret is type Boolean therefore has default value False. The declaration Ret As Boolean = True initializes the parameter with value True. P2R is a private function called from VBA. There is no need for setting optional arguments to non bold in an Excel Function Arguments dialog box (which requires type Variant), nor testing the optional value with VBA IsMissing function
2. Lines 17 and 18: determine the lower (LB) and upper (UB) index numbers of the Price array (assumed to the one dimensional). The example has LB = 0, and UB = 9 (see figure 1)
3. Line 19: Dimension RetArray - the dynamic array for the return values to (LB + 1 to UB) = (1 to 9). Add a second dimension to force column orientation. Option Base 1 was set a line 2, meaning RetArray is Double(1 to 9, 1 to 1) - see figure 1
4. Line 24: Log returns - convert the \(r_{log.t} = log (P_t/P_{t-1})\) formula to a VBA code equivalent with time sub scripts. t = 1 to 9 because the price series is in ascending date order
5. Line 29: Change in price returns \(\Delta P\) - convert the \(r_{delta.t} = (P_t - P_{t-1}) / P_{t-1}\) formula to a VBA code equivalent

1. Figure 2: Constructing the VBA P array in a worksheet

1. Column O: Use 8 digits from the price series O5: =LEFT(D5,8)
2. Column P: Construct the individual P elements using concatenation P6: ="P(" & ROW()-4 & ")"
3. Column Q: Construct the assignment statements Q7: =P7&" = "&ROUND(O7,4)
4. Copy the region with the red frame, and Paste to the VBA code module

Task 1.2: TestP2R

Write a private sub procedure to test the P2R function. Pass the Close vector of the data test period to the function, and set the Optional argument to the default value. The test procedure writes the minimum, maximum and count statistics to the Immediate Window.

'' === B.2

Private Sub TestP2R()
'' Pass a Close vector of prices to P2R
'' Print selected stats to the Immediate Window

Dim P(0 To 9) As Double
Dim RVal() As Double
Const dPlaces As String = "0.00000"

    ' ANZ.AX Close prices 1Jul2016 to 14Jul2016
    P(0) = 23.95
    P(1) = 23.75
    P(2) = 23.4
    P(3) = 22.96
    P(4) = 23.06
    P(5) = 23.12
    P(6) = 23.92
    P(7) = 24.2
    P(8) = 24.5
    P(9) = 24.75

    '' Log returns
        RVal = P2R(P, True)
        '' Write selected stats to Immediate Window
            Debug.Print """RVal = P2R(P, True)"": " & Time
        With WorksheetFunction
            Debug.Print "Return - Min: " & Format(.Min(RVal), dPlaces)
            Debug.Print "Return - Max: " & Format(.Max(RVal), dPlaces)
            Debug.Print "RVal(" & LBound(RVal) & "): " & Format(RVal(LBound(RVal), 1), dPlaces)
            Debug.Print "RVal(" & UBound(RVal) & "): " & Format(RVal(UBound(RVal), 1), dPlaces)
            Debug.Print "Return - Count: " & .Count(RVal) & vbNewLine
        End With

    '' Log returns
        RVal = P2R(P)
        '' Write selected stats to Immediate Window
            Debug.Print """RVal = P2R(P)"": " & Time
        With WorksheetFunction
            Debug.Print "Return - Min: " & Format(.Min(RVal), dPlaces)
            Debug.Print "Return - Max: " & Format(.Max(RVal), dPlaces)
            Debug.Print "RVal(" & LBound(RVal) & "): " & Format(RVal(LBound(RVal), 1), dPlaces)
            Debug.Print "RVal(" & UBound(RVal) & "): " & Format(RVal(UBound(RVal), 1), dPlaces)
            Debug.Print "Return - Count: " & .Count(RVal) & vbNewLine
        End With


    '' Delta returns
        RVal = P2R(P, False)
        '' Write selected stats to Immediate Window
            Debug.Print """RVal = P2R(P, False)"": " & Time
        With WorksheetFunction
            Debug.Print "Return - Min: " & Format(.Min(RVal), dPlaces)
            Debug.Print "Return - Max: " & Format(.Max(RVal), dPlaces)
            Debug.Print "RVal(" & LBound(RVal) & "): " & Format(RVal(LBound(RVal), 1), dPlaces)
            Debug.Print "RVal(" & UBound(RVal) & "): " & Format(RVal(UBound(RVal), 1), dPlaces)
            Debug.Print "Return - Count: " & .Count(RVal) & vbNewLine
        End With

End Sub

About Code 2

1. Details of the P and RVal arrays are shown in figure 3
2. The remainder of the code is straight forward

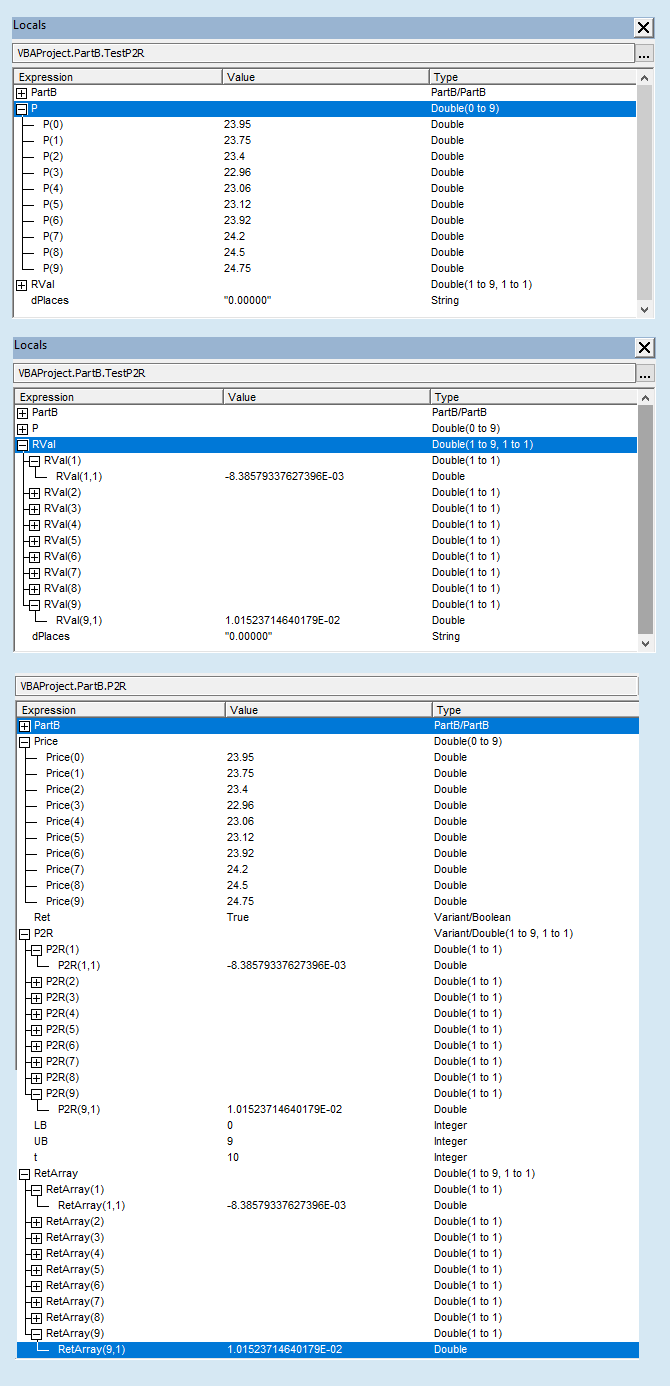
1. lines 64, 78, and 89: Pass arguments by position to the P2R function, and return the "return series" to the RVal array - see figure 3
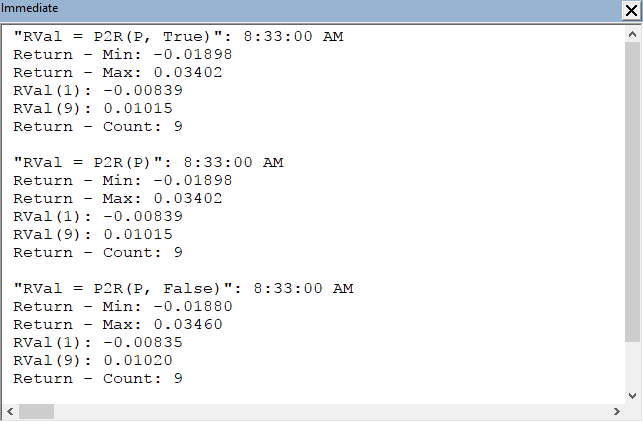
2. The Immediate Window view is shown in figure 4

Task 1.3: Price2Return

Write a User Defined Function (UDF) procedure with the following specifications:

• Name: Price2Return (an abbreviation of Price to Return)
• Arguments:
  1. Compulsory - accepts a Range object, with suitable name and type
  2. Optional - named Ret (the default TRUE for log return, else FALSE for change in price)
  3. Optional - named Asc (the default TRUE for ascending date order data, else FALSE for descending date order data)
• The function is primarily designed to be called from Excel
• Argument 1 will always be an m x 1 column vector, where m is the number of elements
• The return value of "returns" is an array of dimension (m - 1) x 1, suitable for output as an array (CSE) formula
• Test the function on the worksheet. Name the test area TestP2R

In code 3, the Price2Return function is a "wrapper" for the P2R function. This means that P2R is called by Price2Return. The function can be tested from the TestPrice2Return procedure in code 5.

 '' === B.3

Public Function Price2Return(PriceV As Range, _
                             Optional Ret As Variant, _
                             Optional Asc As Variant) _
                             As Variant
'' Price2Return: Price to return
'' PriceV: compulsory - a column vector of prices
'' Ret: optional - a Boolean. True (default) for log return
''                            False for delta price return
'' Asc: optional - a Boolean. True (default) for prices in Ascending order of date
''                            False for prices in Descending order of date
'' Returns an (m - 1) vector of returns
'' User requires knowledge of return vectors to select correct target range for CSE output
Dim inArray() As Double
Dim RValue() As Double
Dim Rtemp() As Double   ' Dimension set by the P2R function return array
Dim t As Integer
Dim r As Integer

    If IsMissing(Ret) Then Ret = True
    If IsMissing(Asc) Then Asc = True

    r = ArrDim(PriceV)
    ReDim RValue(0 To r - 2, 1 To 1)
    ReDim inArray(0 To r - 1)

        If Asc Then
            For t = 0 To r - 1
                inArray(t) = PriceV(t + 1, 1)
            Next t
        Else
            ' Reverse order of prices
            For t = 0 To r - 1
                inArray(t) = PriceV(r - t, 1)
            Next t
        End If

    '' Calculate returns
    Rtemp = P2R(inArray, Ret)

        If Asc Then
                Price2Return = Rtemp
         Else
            ' Reverse order of returns
            For t = 0 To r - 2
                RValue(t, 1) = Rtemp(r - t - 1, 1)
            Next t
                Price2Return = RValue
        End If

End Function

About Code 3

1. Lines 107 to 110 procedure declaration - an Excel UDF with two optional arguments. Use the Optional keyword and type Variant. Default values are handled by the IsMissing functions in lines 125 and 126. The arguments will display in non bold font in the WS Function Arguments dialog box
2. Line 119 declare inArray as a dynamic array of type Double - inArray handles the sort order of the PriceV price vector
3. Line 120 declare RValue as a dynamic array of type Double - RValue handles the Reverse order returns if Rtemp is descending
4. Line 121 declare Rtemp as a dynamic array of type Double - Rtemp stores the Return vector from P2R with values in ascending or descending order
5. Line 128 pass the PriceV range to the ArrDim function. Returns the value 10
6. Line 129 dimension the dynamic array RValue to Double(0 to 8, 1 to 1)
7. Line 130 dimension the dynamic array inArray to Double(0 to 9)
8. Lines 132 to 135 assign the PriceV range values (in ascending order), using row and column index counters to the VBA array inArray
   counter t = 0 to r - 1 :: t = 0 to 9. inArray has base 0, PriceV has base 1
   inArray(t) = PriceV(t + 1, 1).Value :: inArray({0,1,...,8,9) = PriceV({1,2,...9,10}, 1) Note: a VBA array does not have a value property
9. Lines 138 to 140 assign the PriceV range values (in descending order), using row and column index counters to the VBA array inArray in reverse order, ascending, as required by the P2R function
   counter t = 0 to r - 1 :: t = 0 to 9
inArray(t) = PriceV(r - t, 1) :: inArray({0,1,...,8,9) = PriceV({10,9,...,2,1}, 1)
10. Line 144 call the P2R function and assign the return array to the non dimensioned array Rtemp. The assignment dimensions (ReDim's) Rtemp to Double(1 to 9, 1 to 1), the same as the source P2R (see figure 3)
11. Line 147 if prices are Ascending then return the "return vector" to the Caller
12. Lines 150 to 152 if prices are Descending assign the Rtemp returns (in ascending order) as returned by the P2R function, to the VBA array RValue in reverse order, descending, to match the PriceV order
    counter For t = 0 To r - 2 :: t = 0 to 8
RValue(t, 1) = Rtemp(r - t - 1, 1) :: RValue({0,1,...,7,8) = Rtemp({9,8,...,2,1}, 1)

Task 1.4: ArrDim

Write a User Defined Function procedure named ArrDim to return the number of rows in a column vector. The function has one compulsory argument, named Arr of suitable type. The return value should accommodate the maximum row dimension of a worksheet.

'' === B.4

Function ArrDim(Arr As Range) As Variant
' A UDF called from Excel WS
' Count number of rows in column vector
' Returns #Ref error if Arr is not an m x 1 column - additional feature

    If Arr.Columns.Count > 1 Then
        ArrDim = CVErr(xlErrRef)
    Else
        ArrDim = Arr.Rows.Count
    End If

End Function

'' Additional procedure
'' Written in the spirit of code 2

Private Sub TestPrice2Return()

Dim RVal() As Double
Dim Prices As Range

    '' Place 1 of 2:: Uncomment / comment as required - Asc / Desc
    'Set Prices = Range("PriceAsc")
    Set Prices = Range("PriceDes")

    RVal = Price2Return(PriceV:=Prices, Asc:=False)  '' Place 2 of 2 :: Asc / Desc

Stop
End Sub

2. Discussion

As stated in section 1, this module is a code development version, so a number of points are available for discussion.

Q1: Option Base 1 declaration

1. Code 1 line 2 includes the declaration Option Base 1 to set the default lower bound of arrays in the module, but array declarations at lines 19, 47, 129, and 130 explicitly include the lower and upper index number with the To keyword.
Code 1
19 ReDim RetArray(LB + 1 To UB, 1) ' dimension 2: upper index only
Code 2
47 Dim P(0 To 9) As Double
Code 3
129 ReDim RValue(0 To r - 2, 1 To 1)
130 ReDim inArray(0 To r - 1)

2. Is Option Base 1 required?
• In general, the use of Option Base 1 should be avoided. Instead, use the To keyword to explicitly set the lower and upper index numbers of each array dimension. The code can then be read without knowledge of the Option Base declaration. For example, code 3, lines 129 and 130. Pointing the way, Option Base 1 serves no real purpose, and could be deleted. Line 19 should then be written as:
Code 1
19 ReDim RetArray(LB + 1 To UB, 1 To 1) ' dimension 2: indexed 1 to 1 (a single column)

• In this version, however, Option Base 1 is in the module declaration and its impact on the line 19 declaration statement of RetArray is examined next
• The result of the declaration can be viewed in the Locals Window (Expression; Type), see figure 3, and repeated here for reference
• With Option Base 1 set
  RetArray Double(1 to 9, 1 to 1)
• If Option Base 1 is commented out (equivalent to Option Base 0), then RetArray will be (Expression; Type)
  RetArray Double(1 to 9, 0 to 1)
• In other words, removing the Option Base declaration changes the size of the second dimension from one column to two columns
• In this example there is no practical difference, because the population code at lines 24 and 29 includes index 1 for the second dimension
Code 1
24 RetArray(t, 1) = Log(Price(t) / Price(t - 1))
29 RetArray(t, 1) = (Price(t) - Price(t - 1)) / Price(t - 1)

• You just end up with a vector of zeros in the second dimension index 0. See figure 7





3. RValue is declared with a column range "1 To 1", why not simply use "1"?
• The RValue declaration is in line 129
• The logic of the answer is the same as that for RetArray above
Code 3
129 ReDim RValue(0 To r - 2, 1 To 1) ' The array dimension 2 has explicit upper and lower bounds
129 ReDim RValue(0 To r - 2, 1) ' With Option Base 1, this is equivalent to 1 To 1
129 ReDim RValue(0 To r - 2, 1) ' With Option Base 0, dimension 2 is 0 To 1
129 ReDim RValue(0 To r - 2, 0) ' With Option Base 0, dimension 2 is 0 To 0 (equivalent to 1 column)
Option Base 0 is the default and is usually omitted
In the absence of any compelling logic, the choice of base is simply the analysts preference

4. Summary
   • be consistent with Declaration statements involving array dimensions
   • use the To keyword to explicitly declare lower and upper bounds
   • avoid using Option Base, but be aware of it with other code sources

Q2: Code 5 - ascending and descending?

1. Code 5 you have two separate ranges - one for Price descending and one for Price ascending - what is the point of this. Isn't the Price2Return function in code 3 designed to intrinsically sort returns into ascending or descending from a single column vector range of prices (with direction set by Asc argument)?


2. Code 5 is a sub procedure named TestPrice2Return, and as the name suggests this is designed to test (the accuracy of) the Price2Return function by passing range objects:
   • There are two arguments, with four combinations
     1. Ascending :: Log
     2. Ascending :: Change
     3. Descending :: Log
     4. Descending :: Change
   • Yes - the direction can be switched by the Asc argument, but does it give the correct answer?
   • In figure 6, the return vectors for the four combinations are calculated. You can download the workbook to view columns H to N
   • When TestPrice2Return is set to (combination 3 above):
   Code 5
   185 Set Prices = Range("PriceDes")
   187 RVal = Price2Return(PriceV:=Prices, Asc:=False))
   189 Stop
   
   
   
   • The RVal array in the Locals Window can be compared to the WS function values - see figure 8

   

   • This can be repeated for the other combinations, with the inclusion of the Ret parameter
   • The final test is using the UDF Price2Return on a WS - see figure 6

• Thanks to Cosmo for comments
• Download the Excel file for this module: xlf-price2return-v2.xlsm [30 KB]
• Development platform: Excel 2016 (64 bit) Office 365 ProPlus and VBA 7.1
• Revised: Saturday 25th of February 2023 - 10:12 AM, [Australian Eastern Time (AET)]

Copyright © 2011 – 2023 ♦ Dr Ian O'Connor, CPA.   |   Privacy policy

Comment & Reply policy