xlf Extreme Value distributions :: Gumbel

1. Gumbel distribution

Specifications (maximum):

PDF Probability density (mass) function:
- \(f(x) = \frac{1}{\beta} e^{-\frac{x- \alpha}{\beta}} e^{-e^{-\frac{x- \alpha}{\beta}}} = \frac{1}{\beta} exp \left[ - \left( \frac{x- \alpha} {\beta} + exp \left( \frac{x- \alpha} {\beta} \right) \right) \right]\)
CDF Cumulative density function (maximum): \(F(x) = exp \left[- exp \left( \frac{x- \alpha} {\beta} \right) \right] \)
where \(\alpha \) is the location parameter, and \(\beta \) is the scale parameter, \(\beta \gt 0 \)

1.1 Gumbel PDF

Probability density (mass) distribution (figure 1a)

Gembel density — **Fig 1a: Gumbel density mass function -** \(\alpha = 0\), \(\beta = a\) shown in blue

A WS cell formula is provided in figure 1a

Cumulative density plot (figure 1b)

Gembel density WS formula — **Fig 1b: Gumbel density - WS formula** =(1/R30C) * EXP(-( ((RC3 - R29C) / R30C) + EXP(-(RC3-R29C) / R30C) ))

1.1 Gumbel CDF

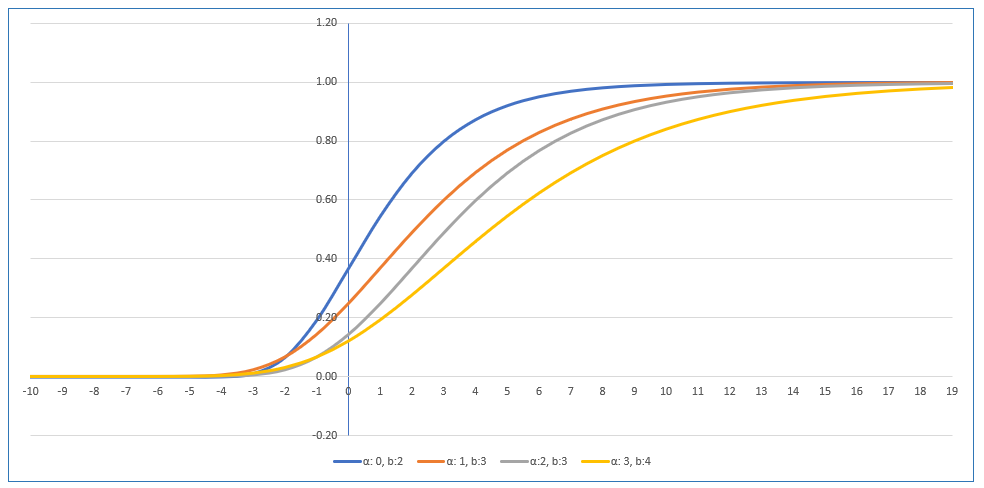
**Fig 2a: Gumbel cumulative function-** \(\alpha = 0\), \(\beta = a\) shown in blue

A WS cell formula is provided in figure 1b

Gumbel cumulative WS formula — **Fig 2b: Gumbel cumulative - WS formula**=EXP(-EXP(-(RC3-R67C)/R68C))

2. VBA :: xlfGumbel function

There is no Excel built-in function for the Gumbel distribution. VBA code is provided in code 1 (xlfGumbel).

Code 1: xlfGumbel function

Function xlfGumbel(X As Double, Alpha As Double, Beta As Double, Cumulative As Boolean) As Variant
Dim tmp As Double
On Error GoTo ErrHandler

    If Beta <= 0 Then GoTo ErrNum

    If Cumulative = True Then
        ' cumulative distribution function
        tmp = Exp(-Exp(-(X - Alpha) / Beta))
    Else
        ' probability mass function
        tmp = (1 / Beta) * Exp(-(((X - Alpha) / Beta) + Exp(-(X - Alpha) / Beta)))
    End If

    xlfGumbel = tmp
    Exit Function
ErrNum:
    xlfGumbel = VBA.CVErr(xlErrNum)
    Exit Function
ErrHandler:
    xlfGumbel = VBA.CVErr(xlErrValue)
End Function

Download the file: xlf-distributions-gumbel.xlsx [31 KB]
This example was developed in Excel 365 version 2007
Published: 31 August 2020
Revised: Saturday 25th of February 2023 - 10:13 AM, [Australian Eastern Standard Time (EST)]