Excel worksheet arrays and vectors


This material about arrays and vectors involves three concepts:

  1. Excel structures able to hold data, most commonly, the array of cells on a worksheet (by reference, name or constant)
  2. mathematical element wise array operations, and
  3. matrix based linear algebra array operations

0. Arrays

An array can be described as a group of items that can be acted on either individually or collectively. An array's orientation is classified by its dimension (such as column orientation, or row orientation, discussed further in section 1). In Excel the concept is best illustrated by example, see figure 1 (worksheet: WS arrays) where "a group of items" means a contiguous range, In particular, an array can be a:

The expressions "scalar", "row vector" and "column vector" are common to the MatLab (matrix laboratory) application software.


array row col multidim
Fig 1: Column, Row and MultiDimensional array - CollArr (6R x 1C), RowArr (1R x 4C), and MDArr (4R x 3C) 12 elements

1. Arrays - concepts


Dimension

The size of an array is described by the number of rows and number of columns. By convention the dimension is always rows first and columns second, in the spirit of R1C1 reference style, and the ordering of row and column arguments in functions such as INDEX and OFFSET.


Excel uses [mR x nR] during selection resizing operations (m and n are common to MatLab). MatLab uses m x n notation, with m being the number of rows (first dimension) and n being the number of columns (second dimension). Thus [2R x 3C] is a 2 row by 3 column array.


An array is contiguous, meaning rectangular / square, and a worksheet array can be referenced by the top left cell and bottom right cell with the range operator, see B11:DF14 in figure 1. Some functions return an array (eg. the TRANSPOSE and MMULT functions).


Dimensions (from figure 1):


In mathematics, the arrays in figure 1 can presented in the form:

$$\text{ColArr}=\begin{bmatrix} r1 \\ r2 \\ r3 \\ r4 \\ r5 \\ r6 \end{bmatrix}, \qquad \text{RowArr}=\begin{bmatrix} c1 & c2 & c3 & c4 \end{bmatrix} \qquad \text{MDArr}=\begin{bmatrix} r1c1 & r1c2 & r1c3 \\ r2c1 & r2c2 & r2c3 \\ r3c1 & r3c2 & r3c3 \\ r4c1 & r4c2 & r4c3 \end{bmatrix}$$

where [ ] represents the array.


Name Manager curly braces "{}"

In Excel there are two representations of arrays:

  1. the worksheet depiction in figure 1, and
  2. computer memory depictions such as the Value and Refers To field of the Name Manager (figure 2)

stored and named constant array
Fig 2: Name Manager - with details of Row, Column, and MultiDimensional arrays (1), and an array constant (2)

Value field

The three arrays from figure 1 are stored arrays link and are labeled in figure 2


In Excel array notation:

  1. Name: ColArr; Value: {"r1";"r2";"r3";"r4";"r5";"r6"}
  2. Name: RowArr; Value: {"c1","c2","c3","c4"}
  3. Name: MDArr; Value: {"r1c1","r1c2","r1c3";"r2c1","r2c2","r2c3";"r3c1","r3c2","r3c3";"r4c1","r4c2","r4c3"}

"Refers To" field

The array ArrConst, labeled in figure 2 is a named array constant. It has 2 x 2 dimension and is used in the Named Array Const worksheet in figure 3.


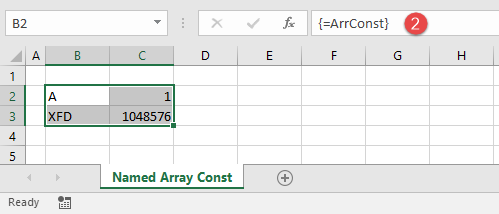
named array constant
Fig 3: Named Array constant - named ArrConst with dimension 2 x 2

In Excel array notation, the named array constant has:

  1. Name: ArrConst;
  2. Value: {...} curly braces with a horizontal ellipses;
  3. Refers To: {"A",1;"XFD",1048576}

To enter the array, select a 2 x 2 range, type =ArrConst in the Formula Bar, then press Control + Shift + Enter to complete the formula.

A named array constant


Function Arguments curly braces "{}"

Array values are displayed in the Function Arguments dialog box to the right of the argument name (figure 4). A maximum of 36 characters are shown.


function arguments curly braces
Fig 4: Function Arguments - with details of Column vector CollArr from figure 2, demonstrated with the COUNTA function

Formula F2 F9 curly braces "{}"

You can check the values in an array (or reference) with the F2 F9 sequence. In figure 5, the cell F2 has the formula =COUNTA(ColArr). To check the values in the array

  1. switch to Edit mode by pressing F2
  2. select the reference ColArr in the Formula Bar
  3. press F9 to debug part of a formula. The result is displayed in the figure
  4. this technique is limited by the formula maximum of 8,192 characters (2 ^ 13)

function arguments curly braces
Fig 5: Formula with an array argument - the Column vector ColArr, in Edit mode (F2) Select F9 to debug part of a formula ie. view the array

2. Arrays - element wise operators


Operations on an array, as described in section 2, requires an array formula which has several distinct features compared to a conventional formula in Excel.


Example - Excel Online #1

From the "element wise" worksheet in figure 6. The example uses two row vectors each of dimension (1 x 3). The range names of the arrays and values are: x = [1,2,3], and y = [4,5,6], and they appear in rows 4 and 5 of figure 6


WS1: the element wise worksheet demonstrates:

  1. Addition
  2. Subtraction
  3. Multiplication
  4. Division
  5. Scalar addition
  6. Scalar subtraction
  7. Scalar multiplication
  8. Scalar division
  9. Scalar exponentiation
  10. Scalar logical

Fig 6: Excel Online #1 - WS1: element by element array operations (1 to 4), and element by scalar constant (5 to 10), WS2: - Units x Price to Sales example. WS3: - 100 records no IF filter WS4: NPV using the VisiCalc handbook numbers and the xlf Carrot Washer example

WS2: The U x P >> Sales worksheet demonstrates a small data base of Unit number and Price data, the user is required to:

  1. Calculate Total Sales using normal cell formulae and the SUM function
  2. Calculate Total Sales using CSE formulae for sales then SUM
  3. Calculate Total Sales using CSE formulae in the final cell
  4. Repeat step 3 using the Excel SUMPRODUCT function

Each vector is 6 x 1.


WS3: The 100 records no IF filter worksheet uses the 100 records data base to demonstrate vector logical CSE formulas. Required:

  1. Sum product A, B and C for Salesperson = "Wong"
  2. Sum product A, B and C for Salesperson = "Wong" AND Month = "September"
  3. Sum product A for Salesperson = "Wong" AND Product A >= 10 AND Product A <= 30

Each field column uses the label as vector name. For example, the Invoice No field has vector name Invoice_No


The CSE formulas are (in Ready mode):

  1. {=SUM((Salesperson = "Wong") * Prod_C_qty)}
  2. {=SUM((Salesperson="Wong") * (Month="September") * Prod_C_qty)}
  3. {=SUM((Salesperson="Wong") * (Prod_A_qty >= 10) * (Prod_A_qty <= 30) * Prod_A_qty)}

WS4: The NPV as CSE worksheet uses using the VisiCalc handbook numbers, and the xlf Carrot Washer example.


The technique is a direct interpretation of the NPV equation - $$\begin{equation} NPV=\sum_{t=0}^{n} \frac{C_t}{(1+k)^t} \end{equation}$$ where the initial cash flow at time zero and future cash flows at time \(t\) are denoted \(C_t\) over \(n\) periods. \(k\) is the periodic discount rate.


Using equation 1, the application is:

The VisiCalc example $$ NPV=\frac{-20,000}{(1+0.1)^{0}} + \frac{3,000}{(1+0.1)^{1}} + \frac{7,500}{(1+0.1)^{2}}+ \frac{15,000}{(1+0.1)^{3}}+ \frac{25,000}{(1+0.1)^{4}}+ \frac{30,000}{(1+0.1)^{5}} = \$35,898 $$

The carrot washer example $$ NPV=\frac{-80,000}{(1+0.05)^{0}} + \frac{10,000}{(1+0.05)^{1}} + \frac{20,000}{(1+0.05)^{2}}+ \frac{15,000}{(1+0.05)^{3}}+ \frac{50,000}{(1+0.05)^{4}}+ \frac{20,000}{(1+0.05)^{5}} = \$17,428 $$


array formula NPV
Fig 7: Formula with an array argument - the Column vector ColArr, in Edit mode (F2) Select F9 to debug part of a formula ie. view the array

The CSE formulas for the NPV estimates are:

  1. VisiCalc =SUM(Cashflows / (1 + Disc) ^ {0;1;2;3;4;5}) returns 35,898.32, where {0;1;2;3;4;5} is an array constant (column orientation 6 by 1)
  2. carrot washer =SUM(Cashflows2 / (1 + Disc2) ^ (ROW(1:6) - 1)) returns 17,427.61