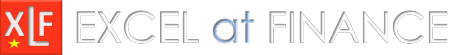Option delta

Black-Scholes model

The Black-Scholes (1973) model states that the theoretical price \(C\) of a European call option on a non dividend paying stock is $$\begin{equation} C=S_0 N(d_1)-Xe^{-rT}N(d_2) \end{equation}$$ where
$$d_1=\frac {log \left( \frac{S_0}{X} \right) + \left( r+ \frac {\sigma^2} {2} \right )T}{\sigma \sqrt{T}} $$ $$d_2=\frac {log \left( \frac{S_0}{X} \right) + \left( r - \frac {\sigma^2} {2} \right )T}{\sigma \sqrt{T}} = d_1 - \sigma \sqrt{T}$$

In equation 1, \(S_0\) is the stock price at time 0, \(X\) is the exercise price of the option, \(r\) is the risk free interest rate, \(\sigma\) represents the annual volatility of the underlying asset, and \(T\) is the time to expiration of the option.

From Put-Call parity, the theoretical price \(P\) of European put option on a non dividend paying stock is $$\begin{equation} P=Xe^{-rT}N(-d_2) - S_0 N(-d_1) \end{equation}$$

Option delta

The change in price of the option contract with respect to the change in the price of the underlying asset is measured by Delta \(\Delta \). It measures the slope of the option price vs underlying asset price curve shown in figure 1. For a call option (the orange curve), delta is
$$\Delta = \frac {\partial C }{\partial S}$$ and is estimated by $$\begin{equation} \Delta_C = N(d_1) \end{equation}$$The delta of a put option is $$\begin{equation} \Delta_P = \frac {\partial P }{\partial S} = N(d_1)-1 \end{equation}$$


Option vs change in stock price
Fig 1: Option price - Call option and Put option for values of S

Suppose that an option has an exercise price \(X\) of $10, the risk-free rate \(r\) is 5% per annum, the volatility of the underlying asset \(\sigma \) is 20%, and that the option expires \(T\) in 1 year. Using equations 1 and 2, the price of a call \(C\) and a put \(P\) option, for stock values \(X\) in the range $5 to $15 is shown in figure 1 \(\Delta = 0.637\).


Delta from first principles

Estimating the slope of the curve from first principles (also referred to in mathematics as the delta method). The x axis is the underlying asset price, and the y axis is the option price, thus, the slope \(m\) is \( \Delta y / \Delta x = (y_2-y_1 )/ (x_2-x_1)\). For a plus and minus one cent change in the underlying asset price around the exercise price of $10.00, (preserving Excel accuracy) \(m= (1.05143603612828-1.03869944030321) / (10.01 - 9.99) = 0.0127365958250678 / 0.02 \approx 0.637\). This is the slope \(\Delta \) of the tangent at \(X=10\) for the call option in figure 1.


The slope of the put curve can be estimated with the same method \(m= (0.553730281135423-0.560993685310354) / (10.01 - 9.99) = -0.00726340417493088 / 0.02 \approx -0.363\).


Option delta
Fig 2: Option delta for a Call option (0 to +1) and a Put option (-1 to 0)

Delta as a Derivative

From equation 3, \(\Delta_C = N(d_1)= 0.636830651175619 \approx 0.637 \) and equation 4, \(\Delta_P = N(d_1) - 1= 0.636830651175619 - 1 \approx -0.363 \).


Option delta in VBA

The VBA code is based on material in the Black-Scholes module. Equations 3 and 4 are implements in rows 14 and 15 of the OptDelta procedure. You can copy code from the code panel, or download the xlsm file from the link at the bottom of this module.



Code 1: Function OptDelta returns the delta for European option on a non dividend paying stock 
Function OptDelta(Stock As Double, _
                  Exercise As Double, _
                  Rate As Double, _
                  Sigma As Double, _
                  Time As Double, _
                  Optional OptType As Variant) As Double
                  ' OptType TRUE (default) for Call, FALSE for Put
Dim d1 As Double, d2 As Double
Dim CallDelta As Double, PutDelta As Double
    If IsMissing(OptType) Then OptType = True
    With Application
        d1 = (.Ln(Stock / Exercise) + (Rate + (Sigma ^ 2) / 2) * Time) / (Sigma * Sqr(Time))
        d2 = (.Ln(Stock / Exercise) + (Rate - (Sigma ^ 2) / 2) * Time) / (Sigma * Sqr(Time))
        CallDelta = .Norm_S_Dist(d1, True)		' equation 3
        PutDelta = .Norm_S_Dist(d1, True) - 1   ' equation 4
    End With
    
    If OptType Then
        OptDelta = CallDelta
    Else
        OptDelta = PutDelta
    End If
End Function

References

Black F, and M Scholes, (1973), The pricing of options and corporate liabilities, Journal of Political Economy, Vol 81 No 3 pp637-654.

Kwok, Y-K, (2008), "Mathematical models of financial derivatives", 2nd ed., Springer.