Quick guide
This is a summary of the rules of exponents material used in the xlf presentation series. It include numerical examples, and keystrokes for the Hewlett Packard 12C financial calculator.
HP 12C RPN keystrokes
Exponents
A exponent is shown as a superscript to a base number – see figure 1.
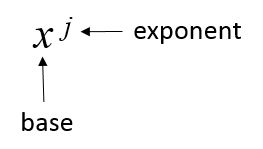
| Exponent rule | Numerical example |
|---|---|
| \(x^0=1\) See Note 1 | \(5^0=1\) \(\text{12c: }5\;[\text{Enter}]\;0\;[y^x]\;\text{returns} \;1\) |
| \(x^1=x\) | \(4^1=4\) \(\text{12c: }4\;[\text{Enter}]\;1\;[y^x]\;\text{returns} \;4\) |
| \(x^{-1}=1/x\) | \(2^{-1}=1/2\) \(\text{12c: }2\;[\text{Enter}]\;1\;[\text{CHS}]\;[y^x]\;\text{returns} \;0.5\) |
| Product rule \(x^j x^k=x^{j+k}\) | \(x^2x^4=x^{2+4}=x^6\) \(2^2\cdot2^4=4\cdot16=64; \quad 2^6=64\) \(\text{12c: }2\;[\text{Enter}]\;2\;[y^x]\;2\;[\text{Enter}]\;4\;[y^x]\;[×]\;\text{returns}\;64\) |
| Quotient rule \(x^j/x^k=x^{j-k}\) | \(x^7/x^3=x^{7-3}=x^4\) \(5^7/5^3=5^{7-3}=5^4=625; \quad 78125/125=625\) \(\text{12c: }5\;[\text{Enter}]\;7\;[y^x]\;5\;[\text{Enter}]\;3\;[y^x]\;[÷]\;\text{returns} \;625\) |
| Power rule \((x^j)^k=x^{jk}\) | \((x^2)^4=x^{2\cdot4}=x^8\) \((4^2)^4=4^8=65536; \quad 16^4=65536\) \(\text{12c: }4\;[\text{Enter}]\;2\;[y^x]\;\;4\;[y^x]\;\text{returns} \;65536\) |
| \((xy)^j=x^jy^j\) | \((xy)^3=x^3y^3\) \((2\cdot3)^3=2^3\cdot3^3=8\cdot27=216; \quad 6^3=216\) \(\text{12c: }2\;[\text{Enter}]\;3\;[×]\;3\;[y^x]\;\text{returns}\;216\) |
| \((x/y)^j=x^j/y^j\) | \((x/y)^2=x^2/y^2\) \((4/5)^2=4^2/5^2=16/25=0.64; \quad(0.8)^2=0.64\) \(\text{12c: }4\;[\text{Enter}]\;5\;[÷]\;2\;[y^x]\;\text{returns}\;0.64\) |
| \(x^{-j}=1/x^j\) | \(x^{-3}=1/x^3\) \(2^{-3}=1/2^3=1/8; \quad2^{-3}=0.125\) \(\text{12c: }2\;[\text{Enter}]\;3\;[\text{CHS}]\;[y^x]\;\text{returns}\;0.125\) |
Note 1: \(\dfrac{x^j} {x^j}=1\), thus by application of the quotient rule \(x^{j-j}=x^0=1\)
The exponential function
The special case where the base \(x\) is set to the mathematical constant \(e, 2.71828\) is important in many areas of finance, such as interest rates in continuous time. The notation \(e^x\) is called the exponential function, and is also written as \(exp(x)\). From the exponent rules, \(exp(1)=e=2.71828\), and \(exp(0)=1\).